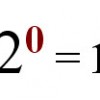Binary Numbers Explained – Beginners Guide

In my experience of teaching networking many students struggle with IP addresses because they lack an basic understanding of binary numbers.

An understanding of binary numbers,the binary system, and how to convert between binary and decimal is essential for anyone involved in computers, coding, and networking.

Binary 101 –  What You will Learn

• The Basics of Number Bases -Base 10, Base 2 and Base 16
• How to convert binary to decimal and vice versa
• How to convert binary numbers to Hexadecimal and vice versa,
• How to convert Hexadecimal to decimal and vice versa,

Overview of Base 10 System or Decimal Numbers

Before we learn about the binary number system we will look in more detail at our normal decimal numbering system.

The principals are the same for all numbering systems, and they are easier to learn using a system that you are more familiar with.

Firstly our decimal system uses 10 as a base and the numbers range from 0 to 9

Let’s look at a few example numbers

We start with the three digit number 129 (one hundred and twenty nine).

This made up of 100 +20 +9 =129

If we look at the diagram below we see that as we move from right to left the columns increase by a factor of 10.

The 2 in the second column isn’t 2 but is 2*10=20 and the 1 in the third column isn’t 1 but 1*10*10=100.

means 10 raised to the power of 0. This is equal to 1 and represents our units column.

The short table below shows a few more entries using the power notation.

When writing decimal numbers we rarely write column values above the numbers as we already know what they are so we simply write:

129 and not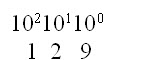

I have introduced the power notation because it is fundamental to understanding binary numbers.

The minimum number possible with three digits is 000 and the maximum is 999. For numbers larger than 999 we need a 4th column which with be the 1000s column.

The Binary Number System

Binary numbers are base 2 numbers, and have only two values – 0 and 1.

If we look at a binary number like 101, then we can again assign column values as we did with our decimal number, but this time we use 2, and not 10 as the base.

So binary 101 binary has 1 in the units column,0 in the 2s column and 1 in the 4s column.

Again if we work our way from right to left then:

The 1 is a 1 as it is in the units column but the next 1 is not 1 but 1*4=4

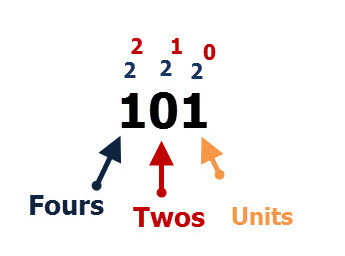
Binary numbers use base 2 and so the columns are

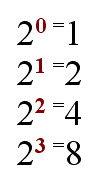
Binary To Decimal Conversion

Let’s look at a few binary numbers and convert them to decimal

We start with the three digit binary number 101 (see image above

The number can be converted to decimal by multiplying out as follows:

1*1 + 0*2 + 1*4 = 5

The maximum value we can have with three binary digits is 111 = decimal 7 calculated as follows-

1*1 + 1*2 + 1*4

More Examples:

1011 binary = 1*1+1*2+0*4+1*8=11

1111 binary = 1*1+1*2+1*4+1*8=15

Try It Yourself

1001 binary = ?

1100 binary = ?

Converting from Decimal to Binary

How do you convert a decimal number to a binary number.

Example what is decimal 10 in binary.

The way I do it is by using the following list of 2 multiples.

128,64,32,16,8,4,2,1

Here’s an handy chart

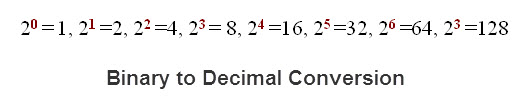
Note: error in diagram above should be 2⁷=128

The procedure is to subtract the number with largest power of two from the decimal number

The largest power of two number that we can subtract is 8 which is 2³.

So 10-8 =2

we now do the same with the remainder so the largest number we can subtract is 2 which is =2¹

2-2=0

so we have 1 eight , No fours, 1 two, No units = 1010 = 2³+ 2¹.

Example 2: Decimal 13 to binary code

1 eight , 1 four, 0 two, 1 units = 1101.

Example 3: Decimal 7 to binary code

0 eight , 1 four, 1 two, 1 units = 0111.

Answers to try it yourself questions

1001 binary = 9

1100 binary = 12

Bytes and Octets and Hexadecimal Numbers

In computers, coding and networking 8 bit numbers are common.

An 8 bit number is known as an octet, and also more commonly it is called a byte. See Wiki for details.

Binary to Decimal and Decimal to Binary Conversion 8 Bit Numbers

An 8 bit binary number can represent a maximum of decimal 255= binary 11111111.

Calculated as follows:

1*128 +1*64+1*32+1*16+1*8+1*4+1*2+1= decimal 255

Here is another 8 bit binary number –01101011.

To convert it to decimal we write the number with the column numbers above, as follows:

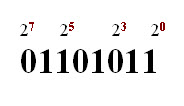
Note: Error in image above should be 2 power 2 and not 3.

if we convert our columns to decimal equivalents using the following chart.

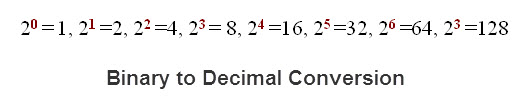
then the binary number 01101011 = 1*1 +1*2+0*4+1*8+0*16+1*32+1*64+0*128

=64+32+8+2+1= 107

Notice it consists purely of 1’s and 0’s.

To convert this number into decimal we need to understand what each 1 represents.

If we write the column values above the numbers then it becomes easy to convert the binary number to decimal.

Decimal to Binary Conversion Example

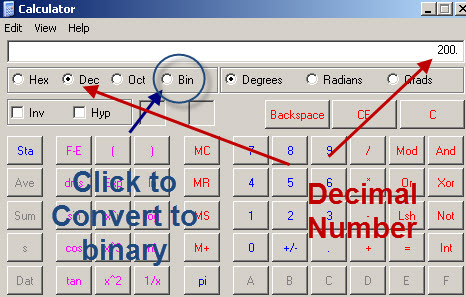
A final larger example convert decimal 200 to binary code

200=128+64+8=2⁷+ 2⁶+ 2³ =11001000

Once you are happy with the process then you can use a binary to decimal calculator like the one on windows.

This converts binary numbers to decimal

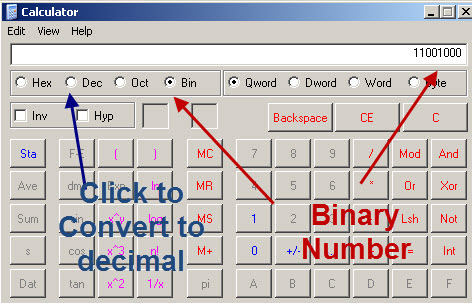
and this converts decimal numbers to binary

Understanding Hexadecimal Numbers

A hexadecimal number (base 16) requires 4 bits and and has a maximum value of 15. It uses the symbols 0-9,A,B,C,D,E,F.

They are represented in binary form as follows:

0000=0
0001=1
0010=2
0011=3
0100=4
..
1010=A
1011=B
1100=C
1101=D
1110=E
1111=F

A byte (8 bits) can be represented as two hexadecimal numbers.

so

FF=binary 11111111 and decimal 255

F0=11110000 binary and decimal 240

 

Video

I produced a video that covers the above if you prefer videos- Understanding Binary numbers video

Workbook

This tutorial is available in pdf format as a workbook and includes more examples. There is a feedback page included with the download were you can comment and request additional help if required.

Resources and Related Articles:

• Good video on binary numbers and conversion
• IPv4 Address classes
• IPv 4 subnetting and Subnet Masks for Beginners
• IPv4 subnetting worked examples
• IPv6 Explained for Beginners
• Beginners Guide to Data and Character Encoding
• JSON Basics For Beginners-With Examples and Exercises